CIMC´2000
The utilization of neuronal nets and genetic algoritms in big databases
MILO ENGOREN, MD
Department of Anesthesiology
St. Vincent Mercy Medical Center
2213 Cherry Street
Toledo, OH 43617
Horse races, football matches, the stock market, intensive care units. People are interested in the outcomes and spend time, effort, and money in modeling the events so as to accurately predict the outcome. This predictive process can be divided into several steps: 1. Create a model.
2. Test the model.
3. Decide if the model is sufficiently accurate.
3a. Not accurate enough: modify the model and go to step 2.
3b. Accurate enough: keep and use the model.
There are many different ways to create models. We are all familiar with statistical models that are used to create APACHE, SOFA, and SPS, amongst others. With the advent of cheap computation, people have developed computer-based algorithms as an alternative or supplement to standard statistical methods. While it would be nice to be able to state when computer-based algorithms should and should not be used, little definitive information is available. Although the thought is the more variables the more likely computer-based algorithms are to be useful. Some of the newer computer based models attempt to imitate how humans supposedly learn and create rules. Artificial neural nets and genetic algorithms are two of these cyber-methods that have received much recent interest for solving difficult problems. Artificial neural nets involve the construction of relationships between variables and then strengthening or weakening the relationships based on feedback – how accurate was the prediction. The focus of this talk will be Genetic Algorithms. Genetic algorithm is a search procedure based by analogy on the principals of natural selection, population genetics, and chromosomal genetics. The goal is that over many generations, the population of models evolves to contain better and better solutions to the problem.
If we try to create a model using height (tall vs. short) and weight (heavy vs. light) to predict outcome, it is easy to enumerate and then test all possible combinations. They are: tall AND heavy predict outcome
tall OR heavy predict outcome
tall AND light predict outcome
tall OR light predict outcome
short AND heavy predict outcome
short OR heavy predict outcome
short AND light predict outcome
short OR light predict outcome
We would then test these eight predictive formulas on our population and see which is the most accurate. If this is a boxing tournament, we may find that tall(er) AND heavy(ier) predict the winner 80% of the time and we may be happy with this result.
However, it becomes increasingly difficult to enumerate and test all possible combinations as the number of variables and the number of categories within each variable increase. If we have four vital signs (heartrate, respiratory rate, blood pressure, and temperature) and four electrolytes (sodium, potassium, chloride, and bicarbonate), we have eight variables. We may want to divide blood pressure not into low, normal, and high; but, into very, very low; very low; low; normal; high; very high; and very, very high. Similarly, if each of the other 7 variables are divided into the same 7 categories, we find that the 7 heartrates can be combined two different ways (AND, OR [IF and NOT can also be used as logical operators, but for simplicity of demonstrating genetic algorithms, I will ignore them]) with 7 blood pressures to produce 98 possible combinations
(1. very, very low heartrate AND very, very low
blood pressure; 2. very, very low
heartrate AND
very low blood
pressure; 3. very, very low heartrate
AND low blood pressure; 4. very, very
low
heartrate AND normal blood pressure; … 97. very, very high heartrate OR very high blood pressure, 98. very, very high heartrate OR very, very high blood pressure.)
Include the other two vital signs and the four electrolytes and we have 7 possible heartrates multiplied by 2 possible (AND, OR) states, multiplied by 7 possible blood pressures, multiplied by 2 possible (AND, OR) states, multiplied by 7 possible respiratory rates etc. and we end up with 78 x 27 = 737,894,528 possible combinations. Three-quarters of a billion possible formulas to evaluate! However, we usually have much more data. We have blood gases, hepatic and renal tests, admitting diagnoses, and comorbidities. We may even have physical examination data. We can include which physician, nurse, and ICU provided the care. Insert a pulmonary artery catheter and add another half-dozen hemodynamic variables. We can rapidly have more possible formulas to evaluate than there are grains of sand in the universe. All these possible formula create what is called the search space.
Using a mixture
of dichotomous (only two possible categories - HAS diabetes mellitus, DOES NOT
HAVE diabetes mellitus), polychotomous (several possible categories – New York
Heart Association Class I, II, II, or IV), and continuous (such as blood
pressure and weight, which are usually divided into several (ten?) categories)
variables, we have worked with more than 10100
possible formulas.
Because we can realistically evaluate only a miniscule fraction (say, 100,000 to 10,000,000 - depending on our computer and the numbers of variables and categories) of these possible formulas, we want to find a way to “home in” on the best formula. With genetic algorithms, we start with a random selection of possible formulas, evaluate these possible formulas, keep the better formulas and change them to try to improve them. We repeat this process until sufficient accuracy can be achieved. This can be described as:
1. CREATION
2. EVALUATION or SELECTION
3. MUTATION and RECOMBINATION.
4. GOTO step 2 until result is sufficiently accurate.
Genetic algorithms must be coded in a computer friendly format. The format I use (and other formats are possible) is to code everything as binary 1’s and 0’s. For example, New York Heart Association would be represented by a gene of 4 binary digits – xxxx, where the first digit represents NYHA I (1000), the second digit represents NYHA II (0100), the third NYHA III (0010), and the fourth NYHA IV (0001). Therefore, 0010 is NYHA III, 0011 is NYHA III or IV, 1010 is NYHA I or III, 1111 is any NYHA class. Here genes represents NOT patient characteristics but predictors in the model. A dichotomous gene, such as diabetes mellitus, would be represented by a gene of a single binary digit, x, where x = 1 if the model includes diabetes mellitus, and x = 0 if the model excludes diabetes mellitus.
Genes are connected by operators, either AND or OR. AND and OR represent their usual BOOLEAN operators. If A AND B are both TRUE, then output is TRUE.
IF A is TRUE AND B is FALSE, then output is FALSE.
IF A OR B (or both) is TRUE, then output is TRUE.
IF Neither A OR B is TRUE, then output is FALSE.
In a logic table, this looks like:
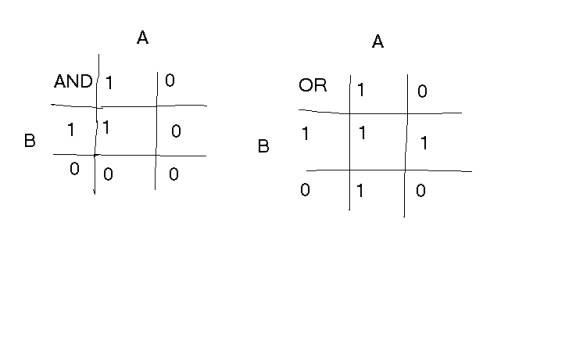
![]()
![]()
![]() where 1 is TRUE and 0 is FALSE.
where 1 is TRUE and 0 is FALSE.
We can now represent some of our 64 possible chromosomes (a chromosome is 2 or more genes connected by operators. There is always one fewer operators than genes) as:
1. 0000 0 0 -> No NYHA class OR has no DM predicts died
2. 0000 0 1 -> NO NYHA class OR has DM predicts died
3. 0001 0 0 -> Has NYHA class IV OR has no DM predicts died
4. 0001 0 1 -> Has NYHA class IV OR has DM predicts died
5. 0001 1 0 -> Has NYHA class IV AND has no DM predicts died
6. 0001 1 1 -> Has NYHA class IV AND has DM predicts died
63. 1111 0 1 -> Has any NYHA class IV OR has DM predicts died
64. 1111 1 1 -> Has any NYHA class AND has DM predicts died
We then test our 64 possible chromosomes on our population:
NYHA DM OUTCOME
1. III yes died
2. I no lived
3. II yes lived
4. none no lived
5. IV yes died
6. III no lived
7. II yes died
8. I no lived
9. I yes died
10. IV yes died
We see that chromosome 1 predicts that patient 1 will live, that patient 2 will die, 3 will live, 4 will die, 5 will live, 6 will die, 7 will live, 8 will die, 9 will live and 10 will live. (It predicts died if either no DM or no NYHA class. It predicts the converse of died (lives) if the patient has both DM and a NYHA class.) Chromosome 1 made only 1 correct prediction. Similarly, chromosome 2 predicts that patients 1, 3, 4, 5, 7, 9, and 10 will die and 2, 6, and 8 will live. Chromosome 2 made 8 correct predictions.
We now expand our chromosomes to contain another two genes: sodium (Na) and PaO2. While normal Na = 140 mEq/L, abnormal values may be considerably higher or lower. Rather than treat this as a polychotomous variable, so that the gene has one site for each possible value (first digit = 1 if Na =1 mEq/L, second digit = 1 if Na = 2 mEq/L, third digit = 1 if Na = 3 mEq/L, up to and perhaps beyond, 200th digit = 1 if Na = 200 mEq/L) we combine the possible Na values into several ranges. While we can do genetic algorithms with giant genes, such as a 200 digit Na gene, this is very memory and time consuming. Additionally, it may lack generalizability. For example, we may have several patients with Na values less than 100 (84, 87, 95, 97, and two at 91) all of whom die. If after constructing and accepting a sufficiently accurate algorithm, we try to predict the outcome of a patient with a Na = 93 mEq/L, we will get a purely random guess, because this particular data point has never been tested. To avoid this, we group large continuous variables into several ranges. For Na, this may be <100, 100 – 109, 110 – 119, 120 – 129, 130 – 139, 140 – 149, 150 – 159, and > 160. The ranges do not have to be equal. We can take the middle three ranges: 120 – 129, 130 – 139, and 140 – 149 and subdivide them into 120 –124, 125 – 129, 130 – 134, 135 – 137, 138 – 142, 143 – 146, and 147 –149, giving us 12 ranges instead of 8. Or, we can construct the ranges so that they have equal number of subjects. This might produce < 115, 115 – 123, 124 – 130, 131- 135, 136 – 139, 140 – 141, 142 – 143, 144 – 147, 148 – 155, > 156. We can even start with one set of ranges and vary the ranges as the algorithm evolves. The Na gene would have 1 digit to represent each range. If we choose to use the last example and have 10 equally populated ranges we might have these following Na genes.
1. 0111001100
2. 1110010101
3. 1010111001
4. 0000000011
5. 1100011010
out of 210 = 1024 possible Na genes.
Gene 1 predicts death if the patient’s Na =115 – 123 OR 124 – 130 OR 131 – 135 OR 142 – 143 OR 144 – 147 mEq/L. Gene 2 predicts death if the patient’s Na = <115 OR 115 – 123 OR 124 – 130 OR 140 – 141 OR 144 – 147 OR > 156 mEq/L. By a similar argument, we would construct ranges for PaO2. (It makes no difference if we use mmHg or kPa as long as we are consistent for all patients. If we forget to convert, we end up like the late NASA Mars mission, where half the software was in pounds and half in Newtons.)
Adding the Na and PaO2 genes to our chromosomes, we now may have:
1. 1010 0 1 1 1110000001 1 1100110000
2. 1100 0 0 1 0000011110 1 1111111000
3. 0001 1 1 0 1111000010 0 1111000001
xxxx a d a yyyyyyyyyy a zzzzzzzzzz
where xxxx is the NYHA gene, d is the diabetes mellitus gene, yyyyyyyyyy is the Na gene, zzzzzzzzzz is the PaO2 gene, and a is the operator between genes. (The spaces between genes and operators spaces are present merely for clarity of demonstration.) At this point there are 228 = 266,338,304 possible chromosomes. You can see that as the number of genes increases, the number of possible chromosomes increases exponentially – rapidly becoming too large to be completely searched for the best chromosome or solution.
We are now ready to start the GENETIC ALGORITHM.
Step 1. RANDOMLY CREATE
CHROMOSOMES CONTAINING THE GENES AND OPERATORS.
Unfortunately our data collectors collected just these four types of information: NYHA class, diabetes mellitus, Na concentration, and PaO2. Using the random number generator on our computer, we randomly create 500 chromosomes of 28 digits each. The optimum number of chromosomes is not known. Some have suggested there should be at least as many chromosomes as digits in the chromosome. Others have suggested that as few as 20-30 is adequate, that more chromosomes just wait computer space and computation time.
Here are several member of Generation Zero.
1010011111000000111100110000
1100001000001111011111111000
0001110111100001001111000001
1110011110110100111110100100
1110011011001111011101011000
1001111110101011001100110101
Step 2. TEST THE
CHROMOSOMES.
Now we need to test these chromosomes. Although the whole population can be used, this is usually done on a portion of the population. If the portion of the population used is “too small,” it introduces too much randomness and variability into what is scored a good solution. While it is nice to use the whole population, there may be limits on computer time, so we must make a tradeoff between population size and the number of generations. For example, if our database contains 50,000 patients, we may choose to use 5000 randomly selected patients on whom to test our chromosomes. In this example, we have been looking at died vs. lived as the dichotomous outcome and it is easy to count accuracy.
In other examples, we may be evaluating a continuous outcome, e.g., for how long someone will live after chemotherapy, rather than number alive at a given time (6 or 12 months). Or, how accurately can we predict cardiac output from capnography? Here accuracy may be measured as the absolute value of the difference between the predicted and actual values.
Predicted Value Measured Value Absolute Difference
3 5 6 3 1
5 4 7 2 3
9 8 8 1 0
15 13 12 3 1
This chromosome predicted survivals of 3, 5, 9, and 15 months when
the actual survivals were 6, 7, 8, and 12 months, for a summed misprediction of
9 months. The
other chromosome predicted survival of 5, 4, 8, and 13 months for a summed
misprediction of 5 months. This is the
more accurate chromosome.
We now test each of our 500 chromosomes against our 5000 patient test population, count the number of correct solutions, and apply “survival of the fittest.” Those with the best accuracy survive. Those that are less accurate die and are no longer used. The proportion who survive (p) is chosen and is typically between 0.1 and 0.25 (10 – 25 %).
Too low survival (low p) and we essentially repeat most of our effort in the succeeding generation. Too much survival (high p) and the chromosomes evolve very slowly. Also, p does not need to be a constant. P can be chosen so that it increases with time as the predictive accuracy of the chromosomes increases. Here we choose p = 0.25, so the best 125 chromosomes survive and the other 375 die.
Step 3. MUTATION AND
CROSS-OVER
Mutation and Cross-over are the two ways that chromosomes evolve. They are very important in that they introduce new members and may search a completely new area of space. With mutation we randomly select a mutation rate (m), which, again, does not need to be a constant, but like p, can vary with the predictive accuracy of the chromosomes. Here, we choose m = 0.1, which means that each digit in the chromosome has a 10% chance of flipping from 0 to 1 or 1 to 0. Usually, mutation rates are about 0.01 (1%) or less.
1010011111000000111100110000 mutates to
1000011111000100111110110000
Crossover is when two chromosomes exchange genetic material.
Chromosome A 1010011111000000111100110000 each gene is a different color
Chromosome B 1100001000001111011111111000 each gene is a different color
Chromosome A 1010011111000000111100110000 colors changed to illustrate crossover
Chromosome B 1100001000001111011111111000
colors changed to illustrate crossover
becomes
1010011101000001111100110000
1100011000000111011111111000
Crossovers need to be of equal length. They do not necessarily have to be of complete genes, nor to they have to be transferred to identical locations. We can even have several cross-overs per chromosome. (not illustrated)
1010011101000001111100110000
1100011000000111011111111000
Here we see that most of the Na gene and one operator of Chromosome A becomes the diabetes mellitus gene, an operator, and most of the Na gene of Chromosome B.
1010011101000001111100110000
1100011000000111011111111000 The underlining shows the transferred material.
We kept 125 chromosomes as survivors so we need another 375 chromosomes to stay at 500. We will get our second 125 by mutating each of the 125 survivor chromosomes. We get the remaining 250 as 125 pairs generated by cross-over. If we kept fewer survivors, we would need to create more by mutation or by crossover to stay at 500 chromosomes.
Step 4 – RETEST – GOTO STEP 2
We now test our new population of 500 chromosomes. We go back to our original population of 50,000 patients and randomly choose 5000 patients as the test subjects. A few of these patients may have been in the previous test group. It doesn’t matter.
We repeat the process of keeping the best chromosomes, mutation, crossover, and retest until we exceed either an arbitrary accuracy or an arbitrary number of generations. After creating our genetic algorithm we have two further problems: overfitting and drift. Overfitting occurs when the model fits the test population “too well” or too specifically. This is similar to using too many variables to describe a curve. It works well until you add a new point or patient. Drift occurs due to changes in care which changes the likelihood of the outcome, such as improving or worsening survival. For example, if we develop a good treatment for renal dysfunction, an elevated creatinine may no longer be a predictor of mortality. Fortunately, most changes in critical care are gradual and incremental. The mortality rate for a particular disease doesn’t halve overnight. (In contrast to a sport event when an injury to the star can have a devastating impact on the team’s success.) For such gradual changes, one can add each new patient to the genetic algorithm’s database and use this new database to predict the next patient’s outcome and let the algorithm repeatedly evolve one (or several) new patient(s) at a time. In theory, one can also program the algorithm to determine on its own which old data to ignore when adding new patients.
Summary
Genetic algorithms are one of several new ways for predicting outcome. While computationally intense, they are easy to implement
SOURCES
http://cs.felk.cvut.cz/~xobitko/ga/ A very nice website that includes JAVA
applets and a tutorial. Also has links
to other genetic algorithm sites.
http://gal4.ge.uiuc.edu/ An University of Illinois site that
offers an on-line course in genetic algorithms.
http://www.iea.com/~nli/ Free demo software for genetic
algorithms that runs in Excel.
http://www.staff.uiuc.edu/~carroll/ga.html A free FORTRAN program for genetic
algorithms. Note: Many genetic algorithms are written in
LISP. Others are written in Pascal or
various versions of C (usually C++), however, any programming language can be
used.
Aleksander I et al. An Introduction to Neural Computing. Chapman and Hall. 1990. Beale R et al. (1990). Neural Computing, an Introduction. Adam Hilger, IOP Publishing Ltd : Bristol. 1990
Congdon CB. A comparison of genetic algorithms and other machine learning
systems on a complex classification task rom common disease research. University of Michigan Thesis. 1995.
Contains a nice glossary of genetic algorithm terms and investigates
the effects of different rules and rates on achieving optimization.
Cross et al. Introduction to neural networks.
Lancet 346:1075-1079, 1995. A
nice blessedly short introduction to neural nets.
Dayhoff JE. Neural Network Architectures: An Introduction. Van Nostrand Reinhold: New York. 1990.
Dybowski R et al. Prediction of outcome in critically ill patients using artificial
neural network synthesised by genetic algorithm. Lancet 347:1146-1150, 1996.
In a small population, the authors found that a neural net based on a
genetic algorithm was more accurate (higher ROC value) than a logistic
regression model.
Freeman JA. Neural networks in Mathematica.
AI Expert Nov:27-35, 1992. Describes
how to write a neural net in Mathematica (a programming language.)
Freeman J.
Simulating a basic genetic algorithm.
The Mathematica Journal 3:52-56, 1993.
Describes how to write a simple genetic algorithm in Mathematica (a
programming language.)
Holland J. Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor, MI, USA. 1975. The seminal book that showed how any problem in adaption can generally be formulated in genetic terms, hence genetic algorithms.
Koza JR.
Genetic programming: on the
programming of computers by means of natural selection. MIT Press, Cambridge, MA, USA. 1992. Genetic programming, which is
hierarchical, is a subset of genetic algorithms.
![]()
![]()
![]() Raich AM et al. Implicit
representation in genetic algorithms using redundancy. Evolutionary Computation 5:277-302,
1997. They introduce a lot of excess
or redundant material into the chromosomes and obviate the need for specifying
the number or location of genes within the chromosome.
Raich AM et al. Implicit
representation in genetic algorithms using redundancy. Evolutionary Computation 5:277-302,
1997. They introduce a lot of excess
or redundant material into the chromosomes and obviate the need for specifying
the number or location of genes within the chromosome.
Tuson A et al. Adapting operator settings in genetic algorithms. Evolutionary Computation 6:161-184,
1998. The authors discuss whether
operator setting (mutation rate, crossover rates, etc.) should be constant or
should vary throughout a given run.
Tsutsui S et al. Forking genetic algorithms:
GAs with search space division schemes.
Evolutionary Computation 5:61-80, 1997.
They describe a new type of GA, which divides the solution space into
subspaces, to improve optimization.
Uuetela K et
al. Global
optimization in the localization of neuromagnetic sources. IEEE Transactions on Biomedical Engineering
45:716-723, 1998. Compares
clustering method, simulated annealing, and genetic algorithms in simulated and
actual magnetic models of the brain.
Vinterbo S et
al. A genetic
algorithm to select variables in logistic regression: Example in the domain of myocardial infarction. Proceedings of the AMIA Annual Symposium
984-988, 1999. Shows that the choice
of variables in a logistic regression model can be improved with the aid of a
genetic algorithm.