
|
Paneles de Discussión
Paneais de Discussio |
Methods for Quantitative Analysis of Ambulatory Blood Pressure MonitoringA. Díez-Noguera*, M.A. Sans-Fuentes*, X. Sarrias**.*Departament de Fisiología, Facultat de Farmacia. Universitat de Barcelona.
5774xsl@comb.es |
|
Name of the interval |
From ... |
... to |
Sys/Dias threshold |
Abbreviation |
|
Day |
Wake up |
Go to bed |
135 / 85 mm Hg |
Day |
|
Short day |
Wake up +1 h |
Go to bed –1 h |
135 / 85 mm Hg |
SDay |
|
First half of the day |
Wake up |
Wake up +6 h |
135 / 85 mm Hg |
1HDay |
|
Second half of the day |
Go to bed –6 h |
Go to bed |
135 / 85 mm Hg |
2HDay |
|
Center of the day |
Wake up +4 h |
Go to bed –4 h |
135 / 85 mm Hg |
CDay |
|
Night |
Go to bed |
Wake up |
115 / 75 mm Hg |
Night |
|
Short night |
Go to bed +1 h |
Wake up –1 h |
115 / 75 mm Hg |
SNight |
|
First half of the night |
Go to bed |
Go to bed +4 h |
115 / 75 mm Hg |
1HNight |
|
Second half of the night |
Wake up –4 h |
Wake up |
115 / 75 mm Hg |
2HNight |
|
Center of the night |
Go to bed +2 h |
Wake up –2 h |
115 / 75 mm Hg |
CNight |
|
After placing short |
After placing |
After placing +2 h |
135 / 85 mm Hg |
SPost |
|
After placing long |
After placing |
After placing +4 h |
135 / 85 mm Hg |
LPost |
This procedure was applied to the original data (previously filtered), then the same procedure was repeated over a data series obtained after fitting the values to a sinusoidal wave by mean of squares regression (Cosinor method 3-4). The equation used is: 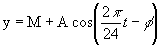 , where y is the variable to be analyzed (S-ABP or D-ABP), t is the time in hours, M is the mesor, or mean value around which the variable oscillates, A is the amplitude of the oscillation and
, where y is the variable to be analyzed (S-ABP or D-ABP), t is the time in hours, M is the mesor, or mean value around which the variable oscillates, A is the amplitude of the oscillation and 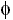 is the acrophase, that indicates the moment of the day at which the function reach the maximum. Knowing the parameters M, A and
is the acrophase, that indicates the moment of the day at which the function reach the maximum. Knowing the parameters M, A and 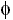 one can generate the new series of estimated data over which the 120 indexes can be calculated. It is important to point out that the new estimated series retains the main characteristics of the original one but eliminates small details and local variations occurred along the day.
one can generate the new series of estimated data over which the 120 indexes can be calculated. It is important to point out that the new estimated series retains the main characteristics of the original one but eliminates small details and local variations occurred along the day.
The last set of indexes is obtained in the same way but analyzing another estimated series of data. In this case we used Fourier analysis to calculate and estimated function containing six sinusoidal functions (harmonics 5-7). In this case the equation is: 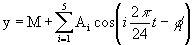 . Similarly to the case of Cosinor analysis, the main characteristics of the original series are retained and also those local changes that are present for intervals longer than four hours.
. Similarly to the case of Cosinor analysis, the main characteristics of the original series are retained and also those local changes that are present for intervals longer than four hours.
As a result of all these calculations 360 indexes were obtained. All these indexes were systematically analyzed calculating means, standard deviations and studying its correlation with the other indexes (Perason’s r). Mean value comparisons were done by the Student’s t test.
Discussion of results and conclusions
Due to the extension of results only some of the must relevant will be discussed. The first thing to discuss is the fact that practically in all overloads calculated from the Cosinor analysis the day-night differences are bigger than those calculate over the original data. This can be explained after considering the details of the calculation: the fitted sinusoidal curve (used for the analysis) normally shows its maximum during the day and the minimum at night. When calculating the area between the curve and the threshold during the night, we have a geometric figure that exaggerates the differences at the extremes of the interval, and consequently the corresponding overload is slightly augmented. Inversely, during the day the overload is reduced. So we see that this method introduces a bias, but, in this case, is a known bias that emphasizes one of the most interesting values: the night overloads.
It is important to point out that all the results obtained for the S-ABP are practically equal to the ones obtained for D-ABP. It is also important to consider the values of thresholds. We used the values commonly recommended in the literature 8, and we observed that there is a tendency to find slightly higher values of overload in the nocturnal intervals of S-ABP. This result clearly suggest that the nocturnal threshold for the S-ABP (115 mm Hg) is probably a bit low, since the overloads calculated on this basis are bigger that the others.
Finally, the commonly used index %D 9-11 has been analyzed studying its correlation with %T, TO and DO. The results show a high correlation between %D and its homologous %T, but they also show that this correlation is reduced when considering the nocturnal intervals. In addition during these intervals the regression coefficient becomes smaller than one, indicating that the values calculated with %D are a bit higher than the real ones obtained with %T. This confirms the convenience of using %T instead of %D, specially at night, when the differences are bigger depending on the methods.
In summary: there are no differences to justify the use of different indexes for the analysis of S-ABP and D-ABP. In general it would be recommendable the quantification of overload on basis to the indexes DO and %T, since their interpretation has a clear biological meaning and shows values much more stables that other indexes currently used, as the %D. The usage of the Cosinor analysis, besides providing information about the amplitude and the acrophase of the circadian rhythm, gives a realistic approximation to the real daily fluctuating values, emphasizing the nocturnal overloads. On the other hand, the stability of the indexes is higher at night, probably due to the increased variability of the recordings during the day.
Bibliography