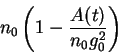Next: Summary Up: Mathematical Modelling and Simulation Previous: Part I: Cardiovascular Risk
Part II: Mathematical Modelling of
Progressive Renal Disease
So far I have discussed a model motivated by renal and patient survival data. The discrete event simulation uses as its motor
three survivor functions: the patient waiting list survivor function, the transplanted patient survivor function and the graft
survivor function. These functions, along with a random number generator and copy of the original 434 patient records allowed
us to test a variety of what if? scenarios. This type of model is of the Monte Carlo type which are widely employed in
the mathematical modelling literature [see, for a discussion, the book by Press et al (1993)]. In essence, what we are
doing is realising numerous real world scenarios. Our only assumption is that our database of 434 records captures the
essential features of the true (yet unobtainable) distribution of renal graft patients in the West of Scotland.
I'd like to present you with another type of model which is one stage more abstract than the one discussed above. We will use differential equations to describe a mathematical model which is not driven by data, as in our discrete event simulation, but which founds itself on a set of fundamental underlying laws.
Let's draw an analogy with fluid flow. Continuum physical theories suggest that force balances and conservation laws must be obeyed by any fluid be it water, blood or air. Consider the entire atmosphere for example. The atmosphere could be completely described if we knew the wind speed and direction at every position above sea-level. But how can we obtain this? We find that the wind velocity is embedded in a force balance between the inertial, pressure gradient, buoyancy and viscous forces. This isn't yet enough to fully extract the wind speed at every point, but if we ensure that the air mass is conserved we are home and dry.
The theory of fluid dynamics has been much developed over the last one hundred or so years, and the hall mark of the subject must surely be the famous Navier-Stokes equations from which we can deduce the flow speed and direction. The equations are not an end in themselves as many situations arise where they are simply too difficult to solve. Mathematical Biology (and more recently, Mathematical Medicine) is a very new subject. Very often, mathematical biologists are, or have had a training in, subjects such as fluid dynamics. However, there is often no coherent mathematical theory for biological processes analogous to that found for fluids. This is certainly the case in renal physiology although some models have been produced. Generally these models are for single nephrons and consist of systems of partial differential equations which do not look so different from the equations for fluid flow! We are interested in renal disease here, but for a description of some of these physiological models (whose future inclusion in disease models is not precluded), see Chapter 20 of the book by Keener & Sneyd (1998), Layton et al (1995) or the special edition of the Bulletin of Mathematical Biology (1994) which was dedicated to renal physiology.
Unfortunately, very little mathematical modelling has focussed on the nature of progressive renal disease. There are many good reviews in the medical literature, e.g.that by Remuzzi & Bertani (1998) or from the book edited by Mitch et al (1986) where there is agreement that the progession to chronic renal failure is independent of the nature of the initial insult. From a simplistic point of view, serving our purposes, any insult leads to nephron loss which induces the release of growth promoting factors. These factors induce glomerular hypertrophy and hence glomerularsclerosis leading to more nephron loss and more hypertrophy. There is hence a runaway snowball effect until chronic renal failure occurs. A strict low protein diet will minimise increased capillary pressure and flow and slow the disease process. But how long can you hold off the devil? In some instances, intervention can be very successful at slowing down the progression of the disease if it is diagnosed sufficiently early.
One mathematical model of chronic renal disease is that by Chaturvedi & Insana (1997) [CI97]. Their work models the progression
of renal disease in an experimental subtotal nephrectomy rat model [Yoshida et al (1989)]. CI97 apply a simple dynamical
systems approach and construct a mathematical model of the disease process in terms of the sclerosis index s [Raij et al
(1984)], the glomerular diameter g and in terms of the number of remaining non-diseased nephrons n. They consider these
quantities only as they vary with time t. By dynamical system they refer to the coupled system of nonlinear ordinary
differential equations:
Here
An important point to note is that the equation for ![]() in (3) is actually decoupled from the other two. Given a set of
initial conditions:
in (3) is actually decoupled from the other two. Given a set of
initial conditions:
CI97 have enjoyed some success with their model. They manage to capture the instantaneous parabolic relationship between
hypertrophy and sclerosis projected by Yoshida et al (1989). However, the model is quite unsatisfactory in many ways.
There are two independent disease mechanisms at work: the first is through equation (3) and the second through
the interplay between ![]() and
and ![]() . Surely,
. Surely, ![]() ,
, ![]() and
and ![]() should all interact simultaneously? Why not simply do without
equation (3) if it is indeed superfluous? CI97 can't! If CI97 simply placed their whole population of nephrons on
the plot
should all interact simultaneously? Why not simply do without
equation (3) if it is indeed superfluous? CI97 can't! If CI97 simply placed their whole population of nephrons on
the plot ![]() at time
at time ![]() all nephrons would become immediately diseased and proceed to total sclerosis regardless of the
initial conditions! Even for a healthy kidney where all the nephrons have initial conditions of
all nephrons would become immediately diseased and proceed to total sclerosis regardless of the
initial conditions! Even for a healthy kidney where all the nephrons have initial conditions of ![]() the model must necessarily
lead to chronic renal failure! Things become even more bizarre as we reach the maximum sclerosed state of
the model must necessarily
lead to chronic renal failure! Things become even more bizarre as we reach the maximum sclerosed state of ![]() . There, sclerosis
continues to increase! In fact,
. There, sclerosis
continues to increase! In fact, ![]() as
as ![]() .
.
What we are in fact alluding to is that there is no equilibrium configuration for nephrons in the model of CI97. Equilibrium or
steady state configurations occur when ![]() ,
, ![]() and
and ![]() cease to vary with time
cease to vary with time ![]() . There, the derivatives must necessarily be
zero. This leads us to a set of equilibrium equations for (1), (2) and (3):
. There, the derivatives must necessarily be
zero. This leads us to a set of equilibrium equations for (1), (2) and (3):
| (5) | |||
| (6) | |||
| (7) |
and there can only be a solution to these equations if
Let's assume that the sclerosis index ![]() is the direct measure of the progressive disease process in a single nephron. Suppose
that any nephron can be in one of two equilibrium states: completely healthy (
is the direct measure of the progressive disease process in a single nephron. Suppose
that any nephron can be in one of two equilibrium states: completely healthy (![]() ) and completely sclerosed (
) and completely sclerosed (![]() ).
Then, if, for a particular nephron,
).
Then, if, for a particular nephron, ![]() is true, then the nephron must be in a transitory state moving between
equilibrium states. We know that once sclerosis has begun we may slow it down with a low-protein diet, for example, so let
us assume that once perturbed from a healthy equilibrium state, the only path is toward a completely sclerosed state with
is true, then the nephron must be in a transitory state moving between
equilibrium states. We know that once sclerosis has begun we may slow it down with a low-protein diet, for example, so let
us assume that once perturbed from a healthy equilibrium state, the only path is toward a completely sclerosed state with
![]() . A good mathematical model of this scenario is the Verlhust-Pearl equation which has been used extensively as a
nonlinear population model. However, here its usefulness is in its two equilibrium states. Let's model the sclerosis index as:
. A good mathematical model of this scenario is the Verlhust-Pearl equation which has been used extensively as a
nonlinear population model. However, here its usefulness is in its two equilibrium states. Let's model the sclerosis index as:
We must now build a model for the glomerular diameter's response to the disease process modelled in ![]() . For simplicity, let's
redefine the variable
. For simplicity, let's
redefine the variable ![]() in the formula:
in the formula:
What does (10) mean? It behaves in much the same way as the equation for sclerosis (8) until
Thus equations (8) and (10) constitute our single nephron disease process model. Any perturbation from the
healthy state (an insult) will send the nephron on a disease path to the sclerosed state as we require. There are in fact two
other equilibrium solutions to our system at ![]() ,
, ![]() and at
and at ![]() and
and
![]() . These are what we call saddle points and we will say some more about them later.
. These are what we call saddle points and we will say some more about them later.
Now that we have our single nephron disease model, how should we make it work for a population of nephrons or for a whole kidney?
We need to bring in the idea of the glomerular filtration rate (GFR). The GFR is proportional to the total available surface
area presented by all the nephrons. Let's call this area ![]() and further suppose that there are initially a population of
and further suppose that there are initially a population of
![]() nephrons in a kidney. Prior to insult, the total glomerular surface area is
nephrons in a kidney. Prior to insult, the total glomerular surface area is ![]() . However, after an insult (e.g.a
subtotal nephrectomy) the new available surface area will be:
. However, after an insult (e.g.a
subtotal nephrectomy) the new available surface area will be:
of nephrons are given random but small perturbations
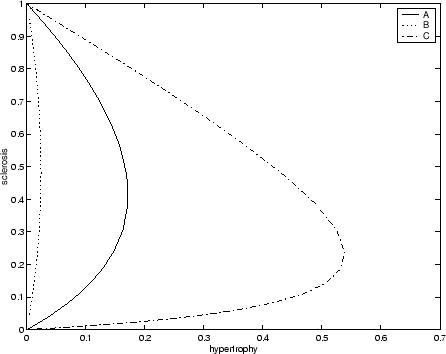 |
In terms of what perturbations to give nephrons, I have illustrated a variety of single nephron disease paths in a plot of
![]() versus
versus ![]() in Figure 5 where I have taken
in Figure 5 where I have taken ![]() and
and ![]() both equal to 1. Note that how, depending on the random
orientation of perturbation, nephrons can become quite hypertrophied before succumbing to sclerosis or only lightly hypertrophied.
Here I suggest that nephrons be selected in a random order onto the disease path and that the degree of the initial perturbation
be of the magnitude of
both equal to 1. Note that how, depending on the random
orientation of perturbation, nephrons can become quite hypertrophied before succumbing to sclerosis or only lightly hypertrophied.
Here I suggest that nephrons be selected in a random order onto the disease path and that the degree of the initial perturbation
be of the magnitude of ![]() but in an random orientation with the
but in an random orientation with the ![]() and
and ![]() axes.
axes.
One unsatisfactory point of this model is that the orientation of the perturbations should not have ![]() . Then, the model will
simply increase the nephron's diameter to
. Then, the model will
simply increase the nephron's diameter to ![]() without increasing
without increasing ![]() . This is due to a saddle-type equilibrium point
which exists for this at the point
. This is due to a saddle-type equilibrium point
which exists for this at the point ![]() and
and ![]() . All we need do to avoid this problem is to ensure that positive
perturbations (no matter how small) are given to both
. All we need do to avoid this problem is to ensure that positive
perturbations (no matter how small) are given to both ![]() and
and ![]() . Finally, one other saddle point exists for my system at the
point
. Finally, one other saddle point exists for my system at the
point ![]() and
and ![]() . However, for positive perturbations, negative values of
. However, for positive perturbations, negative values of ![]() or
or ![]() can never be reached.
can never be reached.
Next: Summary Up: Mathematical Modelling and Simulation Previous: Part I: Cardiovascular Risk
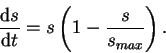
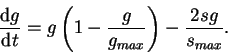
![\begin{displaymath}
A(t) = \sum_{j=1}^{n(t)}[g_0+g_j(t)]^2-n_0g_0^2.
\end{displaymath}](img70.gif)